The key idea to the ProofBlock format is simple: each theorem, postulate and definition is represented by a unique two-dimensional block. When students first start learning, physical manipulatives are typically used, but they quickly transition to drawing each block instead. Each ProofBlock has inputs on the left-hand side, and outputs on the right. The inputs are the information required to use the theorem, postulate, or definition. The outputs are the logical statements the theorem, postulate or definition allow you to conclude.

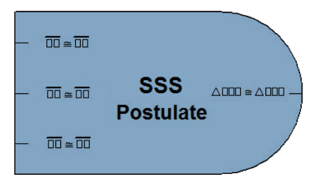
For example, consider the block for the SSS Postulate, shown here. The SSS Postulate states that if three sides of one triangle are congruent to the corresponding three sides of another triangle, that the triangles are congruent.

If we unpack the mathematical language of the postulate, we see that in order to fully satisfy the SSS Postulate's requirements, three separate statements must be true. In particular, given two triangles ∆ABC and ∆XYZ: AB ≅ XY, BC ≅ YZ, and AC ≅ XZ. Therefore, our SSS Postulate block has three inputs, each reading ☐☐ ≅ ☐☐. This gives students knowledge of what form the statements must take, and uses the empty box symbol as a placeholder to indicate where labels from the problem must be inserted.

Continuing our example, the SSS postulate allows one conclusion to be drawn: that ∆ABC ≅ ∆XYZ. Therefore, our block has one output labeled ∆☐☐☐ ≅ ∆☐☐☐, with placeholders ready to accept the information from the problem.

The clear delineation of the "inputs" and "outputs" of each theorem makes it easy for students to create logical arguments. If one block's output matches another block's input, they may be connected, since the conclusion of the first satisfies a requirement of the second. Once all of a block's inputs have been connected, students know the output is true, since the theorem's requirements are all satisfied. Special "Given" and "Picture" blocks allow information from the problem to be included at the beginning of the proof. Once students have a block with an output matching their desired result, and every other block has its inputs fully connected, they know they have completed a logically rigorous proof.



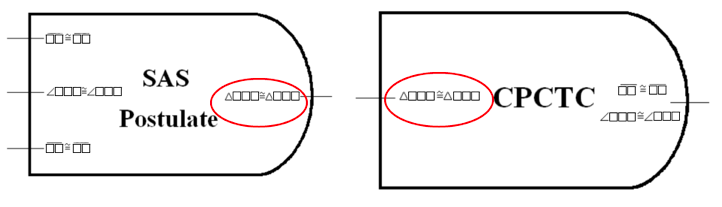
Apart from normal proof problems, ProofBlocks opens a variety of classroom activities to help solidify students' understanding of proof. In some classes, they may be given out purely as a manipulative for introducing proofs. However, more advanced students can be tasked with converting the book's theorems and postulates into blocks themselves, instead of working with pre-created ones. This activity helps to solidify their understanding of each block's requirements and conclusions, while providing practice interpreting mathematical language.

ProofBlocks also transition easily to the more traditional two-column and paragraph proof techniques. A ProofBlock proof contains the same information and rigor as a two-column proof -- it's just displayed in a different manner. While it is excellent for learning the ideas behind creating a logical argument, once students have mastered these skills, they are typically eager to switch to the more concise two-column notation as proofs start to grow longer. However, at this point, they have strong grounding in the concepts behind proof, as well as the requirements and conclusions for their theorems, making them much more capable of success. In addition, there are simple techniques that can be used to convert a ProofBlock proof into a two-column proof, further easing the transition, and helping to show that the same logical argument is being made.

The ProofBlock approach provides many benefits over conventional techniques. By providing students a "toolkit" of ProofBlocks, they have in front of them all of the basic building blocks they need to approach any problem. By separating geometric knowledge from logical reasoning skills, students can focus on the process of proof, rather than becoming distracted by constantly searching through the book for theorems, or parsing the mathematical language of definitions to determine how they are used. Instead, once they have chosen a starting block, they must merely flip through their toolkit to find one with a matching input or output. When working in this manner, proofs may be started from the middle or end far easier than with conventional formats.

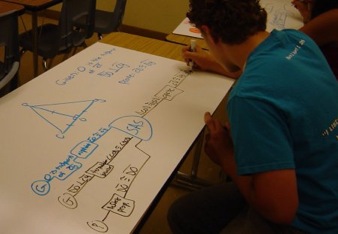
ProofBlocks makes it much easier for students to verify that their own work is correct. This is because it is visually obvious if there are any missing connections (or mismatched connections), making students both more confident and more correct in their results. The ease of tracing the logic through the visual format also facilitates group work and class discussion, especially when work is done on large whiteboards that can be shared between students. ProofBlocks also makes it easier for teachers to make suggestions as to the correct approach without giving away key insights to the proof, since blocks can be suggested, or needed inputs or outputs pointed out.

Being an inherently visual and manipulative based approach, ProofBlocks addresses the needs of students who are often poorly served by traditional teaching methods. Visual learners are well served by seeing the blocks laid out across the page, while the physical manipulatives help connect with kinesthetic learners. English language learners and special education students benefit because the construction of logical arguments does not require strong reading or writing skills as a prerequisite.

The best recommendation for ProofBlocks comes from the students and teachers who have used it. Students find ready success and enjoy building proofs, while teachers find added freedom in the opportunity to guide students toward solutions without spoiling proofs by revealing their key insights. Easy to read, easy to build, and geometrically sound, ProofBlocks make it fun for students and teachers alike to explore logical reasoning in the classroom.