ProofBlocks Introduction Video
ProofBlock Introduction -- The Basics
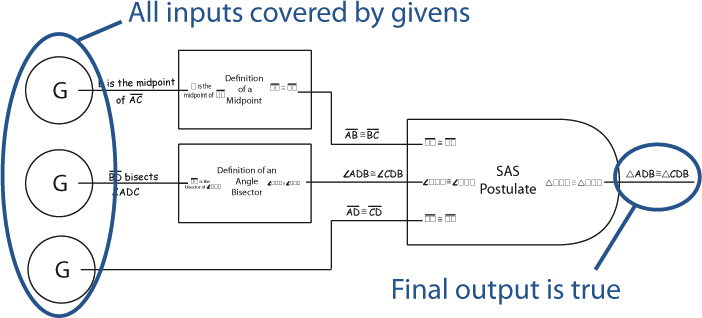
In ProofBlocks, every theorem, postulate, and definition is represented by a block. These blocks can either be physical manipulatives, or simply drawn on the page, depending on student comfort. Below we have the block for the SAS postulate.
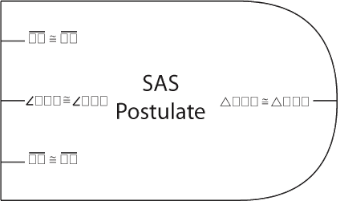
Each block has it's name, a set of inputs, and a set of outputs. Inputs represent information required to use the theorem, postulate or definition, while the outputs represent the information that results from their use.
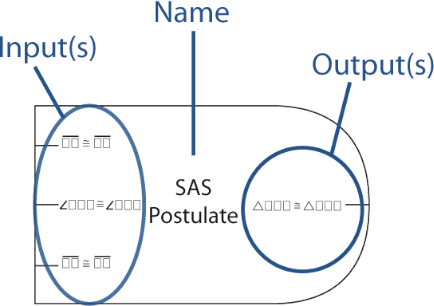
Each input or output is listed in the form it is likely to appear to students. Letters are replaced by a placeholder ☐ symbol. For instance, triangle congruence would be written as ∆☐☐☐ ≅ ∆☐☐☐.
When working on a problem, students will fill in the input and output edges with actual statements from the problem that match the placeholders.
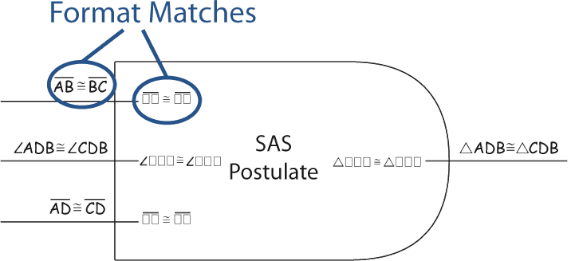
When the output from one block exactly matches the input of another block they can be connected together. This represents the conclusion of the first theorem, postulate, or definition being used to satisfy the hypothesis of the second.
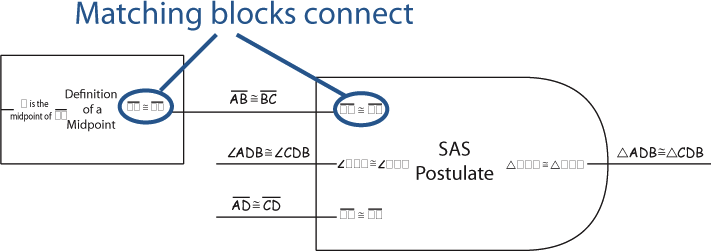
Sometimes the information used by a theorem, postulate or definition comes directly from the picture or the givens. In this case, the "Given" or "Picture" block is used to provide the input.
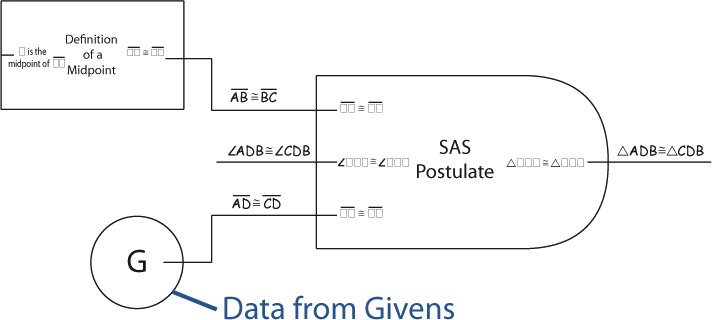
Once all of a block's inputs have been connected, its output is known to be true.
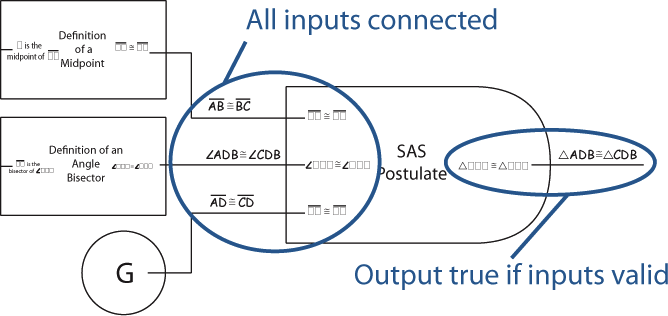
Extending that idea further, we can create entire proofs. Once we have an entire chain of blocks, where there are no missing inputs (everything is covered by a Given, Picture, or fully connected block), and where a block's output matches the desired prove statement, we know that a logical argument has been made.